別記事「食べログの点数の意味とは?データ分析者が知っておくべき4つの尺度」の中で、間隔尺度は平均(算術平均)は求められるのに対して、幾何平均は求められないことを書きました。
この記事の中で、しれっと登場した幾何平均をみなさんは知っていますか?
今回の記事は、
- 幾何平均って聞きなれないけど、何なのか知りたい
- 幾何平均ってどういう場面で使うのかを知りたい
という人に向けて、「幾何平均」が何なのかについて、実例を交えながら紹介していきます。
ファイナンシャルリテラシーがある人なら知っている幾何平均とは?
算術平均と幾何平均の違い
はじめに、算術平均と幾何平均の2つを、簡単に紹介します。
算術平均とは、数値の和をその加えた個数で割った値のことであり、我々が慣れ親しんだ平均値のことです。
一方で幾何平均とは、数値を相乗した値に、その相乗した個数分のN条根をとった値となります。
この説明だけだと、いまいちピンとこないかもしれませんが、算術平均は足し算の平均であり、幾何平均は掛け算の平均とイメージするのがいいかもしれません。
それでは、この幾何平均とは、どういった場面で使われるのでしょうか?

株式・投資信託の世界でも使われる幾何平均
株式・投資信託とトータルリターン
ここ数年、ネット証券の普及や、2018年に開始されたつみたてNISAの制度普及、そして、米国株式の好調な市況などを受けて、米国株式や投資信託などで資産運用を行う人が増えています。
また、その機運とともに、FIRE(Financial Independence Retire Early)をテーマとした書籍が日本国内でも多く出版されるなど、ある種ブームのようなものが起きています。
では、そんな株式や投資信託の世界と、この幾何平均はどのような関係性があるのでしょうか?
投資家が、株式や投資信託などの金融商品を選ぶ際に、最も重視する要素はトータルリターンです。
そして、このトータルリターンをもとに年あたりの平均リターンを求め際に使うのが、 幾何平均なのです。
eMAXIS Slim 米国株式(S&P) の年平均リターン
ここからは、具体例でみていきます。
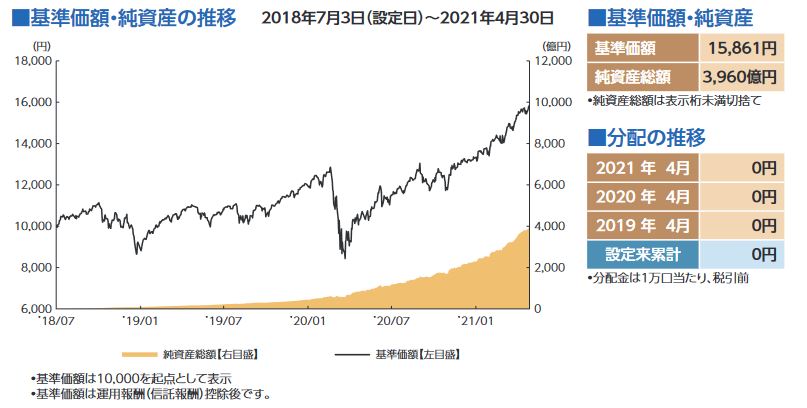
ここでは、三菱UFJ国際投信が販売するeMAXIS Slim 米国株式(S&P)の21年7月の交付目論見書をもとに年あたりの平均リターンを求めていきます。
① トータルリターンを年数で割る方法
2018年7月に基準価額10,000円からスタートしたこの投資信託の2021年4月末時点の基準価額は15,861円であり、この期間のトータルリターンは約58.63%となっています。
この58.63%を(満4年ではないが、集計回数の4回を用い)4で割ると、年あたりのリターンは14.66%となります。そして、この14.66%という収益率で、毎年の収益が均等に増えた場合を考えていきます。
| 年月 | 基準価額 | 収益率 |
|---|---|---|
| 18年7月 | 10,000円 | – |
| 18年12月 | 11,466円 | 14.66% |
| 19年12月 | 13,146円 | 14.66% |
| 20年12月 | 15,074円 | 14.66% |
| 21年4月 | 17,283円 | 14.66% |
最終的な基準価額は17,283円となり、本来の基準価額の15,863円とずれてしまうことが分かり、年あたりの収益率を求める場合は、トータルリターンを年数で割るという方法は間違っているようです。
② 各年の実際の収益率の算術平均を求める方法
次の表は、eMAXIS Slim 米国株式(S&P)の年末の基準価額と、前年比の収益率を示したものです。
| 年月 | 基準価額 | 収益率 |
|---|---|---|
| 18年7月 | 10,000円 | – |
| 18年12月 | 9,230円 | -7.7% |
| 19年12月 | 12,595円 | 30.5% |
| 20年12月 | 13,286円 | 10.3% |
| 21年4月 | 15,863円 | 19.3% |
この各年の収益率に対し算術平均を求めると13.125%となります。
そして、さきほど同様この13.125%という収益率で、毎年の収益が均等に増えた場合を考えていくと、、、
| 年月 | 基準価額 | 収益率 |
|---|---|---|
| 18年7月 | 10,000円 | – |
| 18年12月 | 11,313円 | 13.125% |
| 19年12月 | 12,797円 | 13.125% |
| 20年12月 | 14,477円 | 13.125% |
| 21年4月 | 16,377円 | 13.125% |
最終的な基準価額は16,377円となり、本来の基準価額の15,863円とずれてしまうことが分かります。やはり、年あたりの収益率を求める際に、毎年の収益率の算術平均で求める方法も間違いのようです。
③ 幾何平均で求める方法
それでは、最後に幾何平均を用いて、年あたりの収益率を求めていくことを考えていきます。
今回の投資信託の収益率の例を数式で表すと、次のように表すことが出来ます。
$$\begin{align}
(N年後の基準価額) = & (初年度の基準価額) × \{1+(1年後の収益率)\} ×\\ & \{1+(2年後の収益率)\} × … × \{1+(N年後の収益率)\}\\ \\= & (初年度の基準価額)×\{1+(幾何平均)\}^N\end{align}$$
そして、この式を変形すると、
$$\begin{align}\frac{(N年後の基準価額)}{(初年度の基準価額)} = & \{1+(幾何平均)\}^N\\
\sqrt[N]{\frac{(N年後の基準価額)}{(初年度の基準価額)}}= & \{1+(幾何平均)\}\\\\
(幾何平均) = & \sqrt[N]{\frac{(N年後の基準価額)}{(初年度の基準価額)}} – 1
\end{align}$$
と表すことが出来ます。
ここで、今回の例の、eMAXIS Slim 米国株式(S&P)の数値を当てはめると、次のように幾何平均が12.227%と求めることが出来ました。
$$(幾何平均) = \sqrt[4]{\frac{15,863円}{10,000円}} – 1 = 0.12227 = 12.227[\%]$$
そして、さきほど同様に、求めた12.227%という収益率で、毎年の収益が均等に増えていく場合の最終的な基準価額を求めていくと、、、
| 年月 | 基準価額 | 収益率 |
|---|---|---|
| 18年7月 | 10,000円 | – |
| 18年12月 | 11,223円 | 12.227% |
| 19年12月 | 12,595円 | 12.227% |
| 20年12月 | 14,135円 | 12.227% |
| 21年4月 | 15,863円 | 12.227% |
最終的な基準価額は15,863円となり、目論見書で報告されている基準価額の15,863円と合致しました。
つまり、年あたりの収益率を求める場合は、幾何平均を用いるのが正しいことが確認できました。

幾何統計は統計検定2級でも出題
最後に、これはおまけの話ですが、統計検定2級において、幾何統計に関する問題は過去にも出題されています。
- 2018年6月 第10問
- 2021年6月 第2問
統計検定2級の試験では、関数電卓を使用することはできず、一般的な事務電卓の使用のみ認められているため、N条根は求めることができず、求められるのは平方根だけとなります。
そのため、実際の試験では、今回紹介した例のようにN条根のNの値は4となり、
$$\begin{align}(幾何平均) & = \sqrt[4]{\frac{15,863円}{10,000円}} – 1 \\ & = \sqrt{\sqrt{\frac{15,863円}{10,000円}}} – 1 = 0.12227 = 12.227[\%]\end{align}$$
といった具合に、平方根を2回行うことで4乗根を求めさせるような出題パターンであったりします。
試験本番でN条根を求める問題が出題されると一瞬焦りますが、これは、解き方のコツだけを知っておけば、本番で出題されても焦ることはないと思いますので、このコツをここで覚えておきましょう。
まとめ
今回の記事では「ファイナンシャルリテラシーがある人なら知っている幾何平均とは?」と題して、幾何平均が何なのかを、株式・投資信託の話を絡めてご紹介していきました。
この幾何平均については、聞きなれない言葉ではありますが、我々が日常で触れている数字でもよく使われていることから、その求め方を理解しておいても損はないと思います。
じゃあ