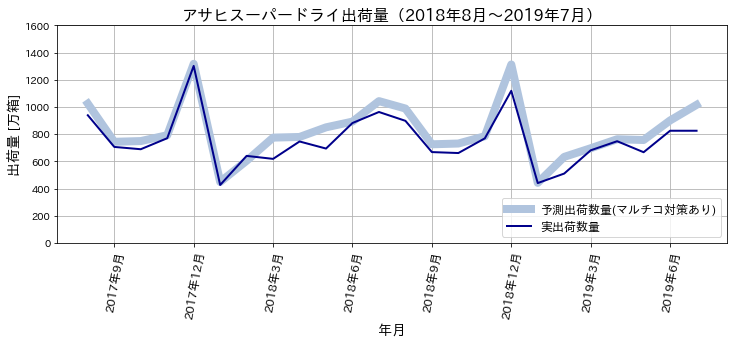
別記事「重回帰分析で将来のビール出荷量を予測してみた」では、重回帰分析を用いてスーパードライの将来の出荷量を予測する方法について紹介していきました。
そして、1年前の出荷数量のデータを用いることで、将来のスーパードライの出荷数量の予測精度を上げられることを紹介しました。
しかし、得られた回帰分析の結果は、多重共線性の問題を抱えていることも書きました。
ということで、今回の記事では、
- 重回帰分析を行う際に注意すべき多重共線性について知りたい
- 分析の過程で発生する多重共線性にどう対応していくのかに興味がある
という人に向けて、前回の記事に引き続き、スーパードライの出荷数量の回帰分析の過程で発生した多重共線性についての説明と、それを解消させるまでの過程と結果について紹介していきます。
重回帰分析で発生する多重共線性に対処してみた

多重共線性(マルチコ)とは?
はじめに、多重共線性(Multicolliniarity:モルチコ)について説明します。
重回帰分析では複数の説明変数を用いて回帰分析を行うことになるわけですが、この際に用いる複数の説明変数において、互いに相関が強い関係にある説明変数が複数ある状態を、多重共線性があるといいます。
そして、多重共線性がある状態で分析を進めると、誤った分析結果となるリスクがあります。
この「誤った分析結果となる」という点について、具体例を挙げて説明していきます。
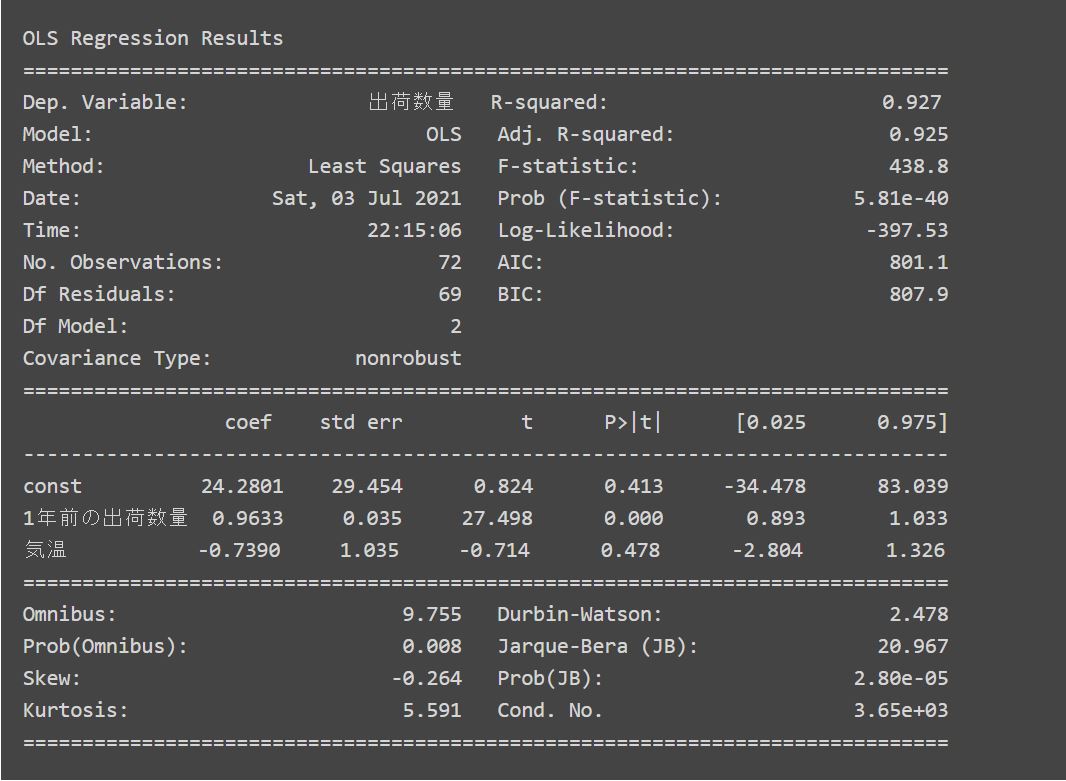
上のログは、スーパードライの出荷数量を「気温」と「1年前の出荷数量」の2つの説明変数のみで回帰分析させた場合の統計サマリとなります。
気温の回帰係数を見ると、マイナス0.739となっていることが分かります。
これは、気温が1度上がるごとに、スーパードライの出荷量が0.739ケース減少することを示唆することになります。
しかし別記事「気温が上がるとビールの出荷量は増えるのか?」で分析&紹介した通り、気温とスーパードライの出荷数量の間には正の相関があるため、その傾向とは真逆の結果となります。
この例のように、多重共線性がある場合は、説明変数が本来もつ傾向とは異なる傾向(回帰係数)となってしまう可能性があるため注意が必要となってきます。
多重共線性の評価から改善までの道のり
① 多重共線性を評価する方法は?
多重共線性がよくないことはわかりましたが、多重共線性が発生しているかどうかは、どのような方法で確認すれば良いのでしょうか?
多重共線性を評価する手法のひとつに、VIF(Variance Inflation Factor: 分散拡大要因)と呼ばれる指標があります。
VIFは以下の式で求められます。
VIF = 1/(1-R2) ※ R2 : 各説明変数の決定係数
ここでの各説明変数の決定係数とは、注目したい説明変数を目的変数とみなし、それ以外の説明変数で回帰分析を行った際に得られる決定係数のことを指します。
よって、ある説明変数を、それ以外の説明変数で説明できるのであれば、その説明変数は不要であることを示唆することになります。
ということで、前回の分析で用いた説明変数のVIFを求めてみました。
| 各説明変数 | VIF factor |
|---|---|
| 気温 | 79.05 |
| 1年前の出荷数量 | 26.14 |
| 月_10月 | 46.28 |
| 月_11月 | 33.24 |
| 月_12月 | 69.75 |
| 月_1月 | 10.25 |
| 月_2月 | 16.16 |
| 月_3月 | 29.50 |
| 月_4月 | 38.02 |
| 月_5月 | 53.36 |
| 月_6月 | 66.15 |
| 月_7月 | 93.25 |
| 月_8月 | 94.80 |
| 月_9月 | 65.31 |
ここで、多重共線性を判断する明確なVIF基準値は決まっていないようですが、一般的には10未満であることが求められるようです(さらに厳しい場合は、5未満や4未満などの基準もあるようです)
今回の結果では、ひとつもVIF10未満を満たす説明変数がない状態となっているため、多重共線性を抑えるため、不要な説明変数を減らす必要が出てきました。
ここで、各説明変数間の相関関係を確認するために、相関係数行列を求めていきます。
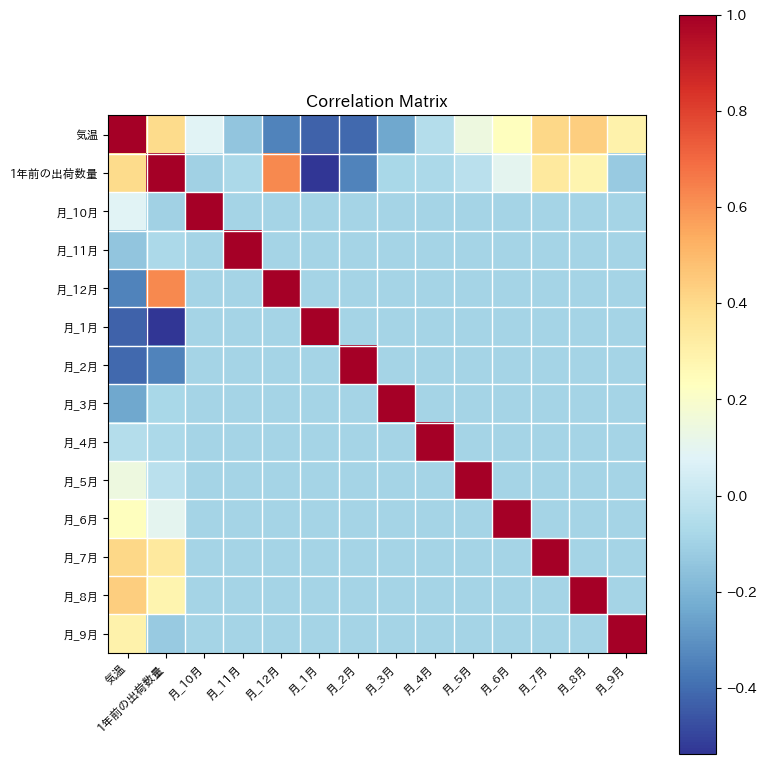
この結果より、各月同士の相関は弱いことが分かりましたが、「気温」「1年前の出荷量数量」と他の説明変数の間には相関があることが分かります。
② 多重共線性を抑えるために説明変数を減らす
多重共線性を抑えるために、説明変数を減らしていくことを考えていきます。
VIFの値が大きい説明変数を除外させることで、多重共線性を抑えることができそうですが、まずは、VIFの値が大きく複数の説明変数との相関係数が大きい「気温」を、説明変数から除外していくことを考えていきます。
まずはVIFの確認から行います。
「気温」を説明変数から除外したVIFの結果は次の通りとなります。
| 各説明変数 | 元のVIF | 見直し後のVIF |
|---|---|---|
| 気温 | 79.05 | – |
| 1年前の出荷数量 | 26.14 | 23.39 |
| 月_10月 | 46.28 | 25.29 |
| 月_11月 | 33.24 | 26.43 |
| 月_12月 | 69.75 | 69.70 |
| 月_1月 | 10.25 | 8.41 |
| 月_2月 | 16.16 | 15.56 |
| 月_3月 | 29.50 | 26.29 |
| 月_4月 | 38.02 | 26.45 |
| 月_5月 | 53.36 | 28.65 |
| 月_6月 | 66.15 | 35.38 |
| 月_7月 | 93.25 | 49.22 |
| 月_8月 | 94.80 | 45.90 |
| 月_9月 | 65.31 | 24.02 |
それぞれの説明変数が10未満となっていないので、まだ多重共線性が強いことになります。
そのため再び相関係数行列の確認を行います。
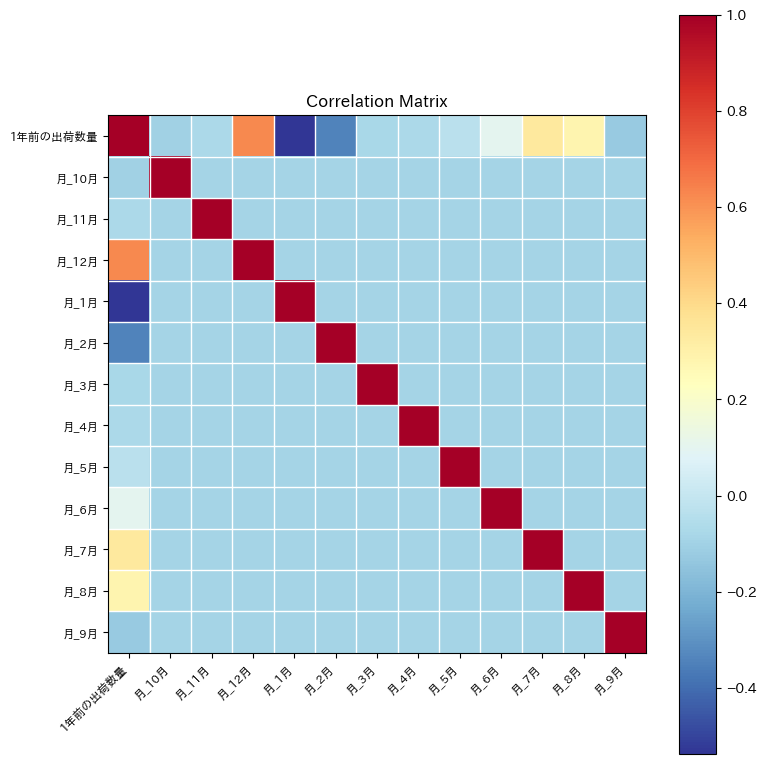
ここで、「1年間の出荷数量」が他の説明変数との相関が強いことが分かります。
しかし、「1年間の出荷数量」を説明変数から除外させてしまうと将来の予測するための時系列のトレンドを見れなくなってしまうため、ここではVIF値と相関係数が高い「月12月(12月ダミー)」を説明変数から除外していくことを考えていきます。
さきほどの状態から「月12月(12月ダミー)」を説明変数から除外したうえで、VIFを求めた結果は次の通りとなりました。(見直しVIF②)
| 各説明変数 | 元のVIF | 見直しVIF① | 見直しVIF② |
|---|---|---|---|
| 気温 | 79.05 | – | – |
| 1年前の出荷数量 | 26.14 | 23.39 | 5.33 |
| 月_10月 | 46.28 | 25.29 | 1.35 |
| 月_11月 | 33.24 | 26.43 | 1.36 |
| 月_12月 | 69.75 | 69.70 | – |
| 月_1月 | 10.25 | 8.41 | 1.12 |
| 月_2月 | 16.16 | 15.56 | 1.20 |
| 月_3月 | 29.50 | 26.29 | 1.36 |
| 月_4月 | 38.02 | 26.45 | 1.37 |
| 月_5月 | 53.36 | 28.65 | 1.40 |
| 月_6月 | 66.15 | 35.38 | 1.49 |
| 月_7月 | 93.25 | 49.22 | 1.69 |
| 月_8月 | 94.80 | 45.90 | 1.64 |
| 月_9月 | 65.31 | 24.02 | 1.33 |
自分でもちょっと驚きましたが、一気にすべての説明変数のVIFを10未満とすることができました。
これで多重共線性のリスクを抑えた回帰式を得ることができそうです。
③ 多重共線性を抑えた回帰分析の結果は?
「気温」と「月_12月(12月ダミー)」の2つの説明変数を除外することで、多重共線性を抑えられることが分かったため、この2つの説明変数を除外したうえで重回帰分析を行っていきます。
そして、重回帰分析の結果は次のようになりました。
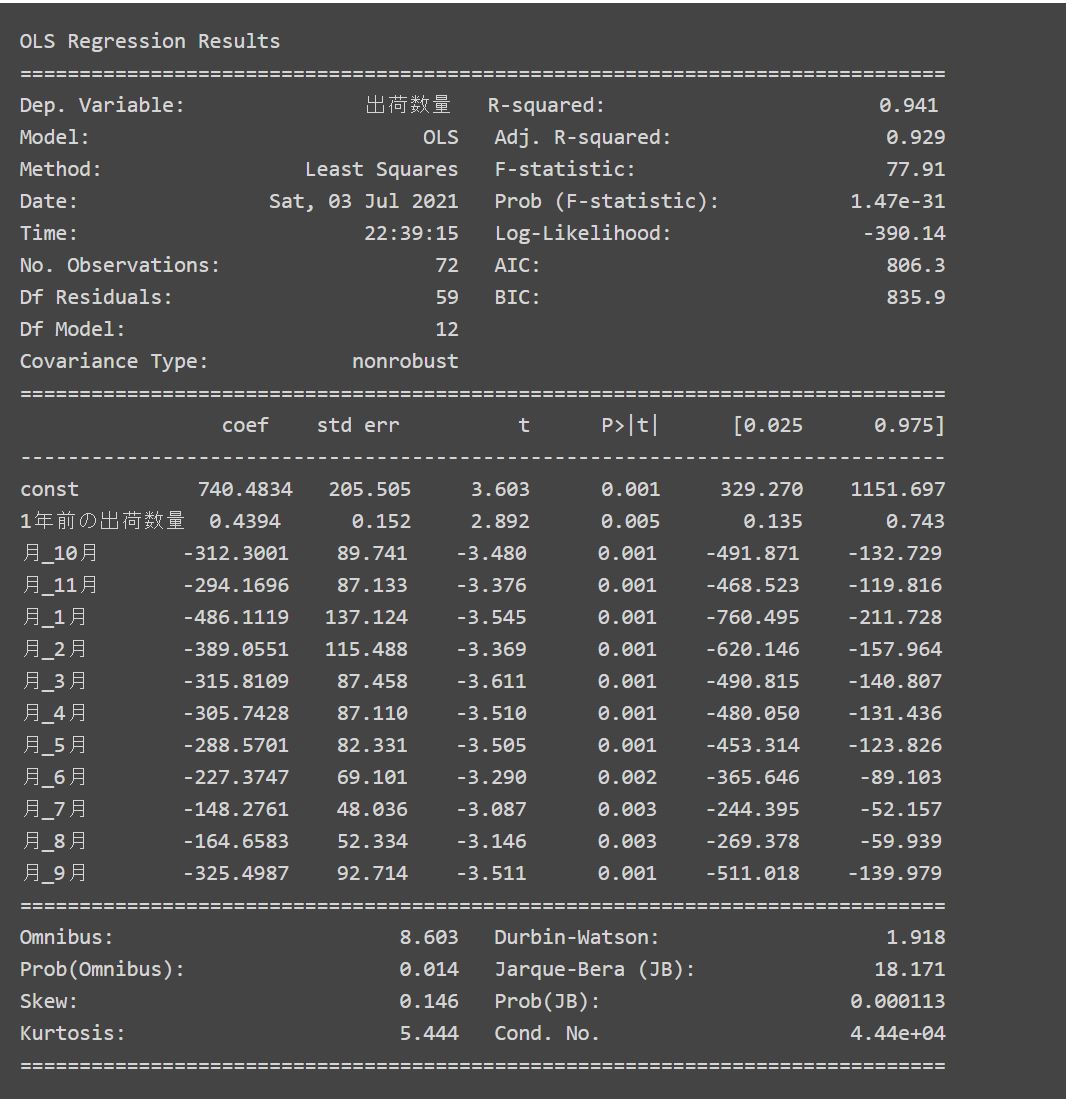
別記事「重回帰分析で将来のビール出荷量を予測してみた」で求めた重回帰分析の結果と比較してみると、
- 自由度調整済み決定係数(Adj. R-squared)が0.927から0.929と改善
- 条件数(Cond. No.)も1.87e+19から4.44e+04と大きく改善
- すべての説明変数のP値も0.05未満となる
という結果となり、多重共線性のリスクを抑えた状態で、高い有意水準の回帰式を得ることが出来ました。
多重共線性を抑えるために説明変数を除外しましたが、結果的に、各回帰係数のP値もすべてクリアできた点は、予想をしていなかっただけに驚きました。
それでは最後に得られた回帰式で描かれれる出荷数量のグラフを示して終わりとします。(誤差などの評価は割愛)
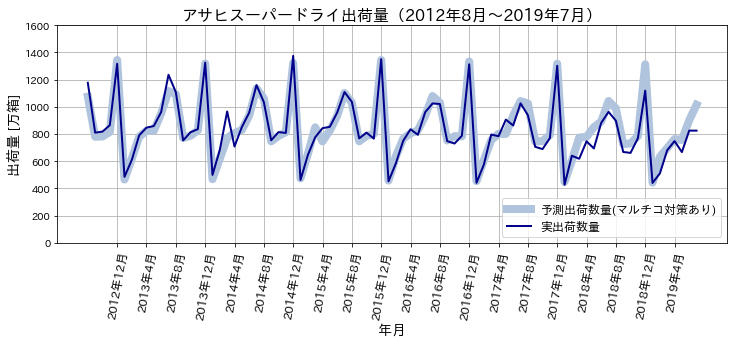
まとめ
今回の記事では「重回帰分析で発生する多重共線性に対処してみる」というテーマで、スーパードライの出荷数量の回帰分析で発生した多重共線性についてと、それを解消させるまでの過程について紹介していきました。
多重共線性(マルチコ)がある状態で分析を進めると、誤った分析結果となってしまうリスクがあることを紹介しました。
そして、VIF(分散拡大要因)と呼ばれる手法で多重共線性を評価していき、相関行列なども用いて、不要な説明変数を除外させることで、多重共線性のリスクを抑えることが出来たことを、その過程とともに紹介していきました。
重回帰分析を行う際は、はじめにP値に注目してしまう人もいるかもしれませんが、先に多重共線性を評価したほうが、最適な分析結果に早くたどり着くのかもしれません。
私たちは20代から50代のビジネスパーソンに向けて、パラレルキャリア研究会というコミュニティーを運営しています。当研究会はデータサイエンスについても互いに学び合う場を提供しています。
私達と一緒に学んでみたいという意欲のある方、データサイエンスの自学自習に少しでも興味がある方は、お気軽にこちらからお問い合わせください。
じゃあ