別記事「重回帰分析で求められるビールの出荷量の予測精度は?」では、過去の複数の説明変数を用いた重回帰分析で、ビールの出荷量を求めました。
そして、おおよそ±12%の誤差範囲で、ビールの出荷数量を予想できる結果を得ました。
しかし、前回紹介した分析のアプローチでは将来の出荷数量予想には適した分析ではないことも紹介しました。
ということで、今回の記事では、
- 重回帰分析による将来予想法について興味がある
という人に向けて、重回帰分析でスーパードライの将来の出荷量を予測していく方法について紹介していきます。
重回帰分析でスーパードライの将来の出荷量を予測してみる

将来予測に時系列分析を用いてみる
① 前回の重回帰分析手法が将来の予想に適さない理由
前回「重回帰分析で求められるビールの出荷量の予測精度は?」の分析では、
- 平均気温
- 月データ(月ダミー)
- 年データ(年ダミー)
の3つデータを用いて重回帰分析を行いました。
ここで、過去のデータを用いる場合であれば、それぞれの年の回帰係数を求めることができるのですが、データのない将来の年の回帰係数は求めることができません。
したがって、将来の予測において、年データ(年ダミー)は分析に適さないデータということになります。
それでは、もし「年データ(年ダミー)」を使わずに、重回帰分析を行うと、どのような結果となるのでしょうか?
なお、今回の分析では、将来の出荷数量を予想するというテーマを設定しているため、重回帰分析に用いる学習用データとしては2011年8月から2018年7月までのデータを用いることとし、2018年8月から2019年7月までのデータは、予実を比較するためのテストデータとし学習用データからは除外したうえで分析を行っていきます。
ということで、次のグラフが、年ダミーなしで重回帰分析を行い、その結果より予想出荷量を折れ線グラフで表したのグラフとなります。

このグラフより、特に2018年以降で、予想と実際の数量の誤差が大きくなる結果となり、月ごとの出荷数量の増減の傾向は捉えられてはいますが、全体的に出荷量を多く予想する結果となってしまいました。
それでは、将来の出荷数量を予測精度を改善させるためには、どのような分析アプローチをとればいいのでしょうか?
② 時系列分析における周期性の可視化手段コレログラム
改めて、今回のスーパードライの出荷量の推移をみると、同じような形の折れ線グラフが繰り返し発生しており、周期性があることが読み取れます。
そのため、この周期性に着目して分析を行うことを考えます。
時系列分析における、周期性を可視化する手段としてコレログラム(Correlogram)と呼ばれる手法があります。
そして、次のグラフはスーパードライの出荷量のコレログラムを描いたものです。
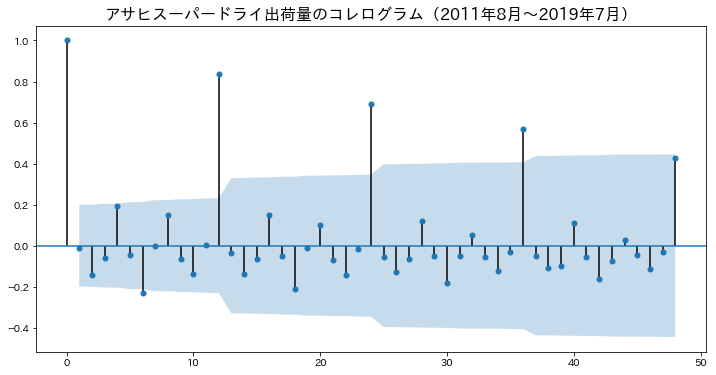
このコレログラムは、
- 横軸:元データから時間のズレ量(ここでの単位は月)
- 縦軸:元データと元データから時間をずらしたデータとの相関係数(自己相関)
をとっており、この結果から、データの周期性(自己相関性)を見ることができます。
そして、このコレログラムでは、横軸の12(12か月のラグ)の位置の自己相関の値が大きいことから、ある月の出荷数量は12カ月前の出荷数量と相関が最も高いと言うことができます。
この結果を踏まえて、12カ月前の出荷数量データを回帰分析に用いることを考えていきます。
③ 12か月前のデータを用いた回帰分析
12か月前の出荷数量データを回帰分析の新たな説明変数としたうえで分析を行います。
12か月前の出荷数量データを新たな説明変数に加える方法を言葉で説明すると、エクセルでイメージした場合、
- オリジナルの出荷数量の列データをコピーする
- 新たな列にコピーしたデータを下方向に12セルずらして貼り付けを行う
といった、イメージです。
Pythonで処理する場合は、1行の記述でこのデータ操作を実現できます。
さて、説明変数を加えた後の重回帰分析のサマリを見ていきます。
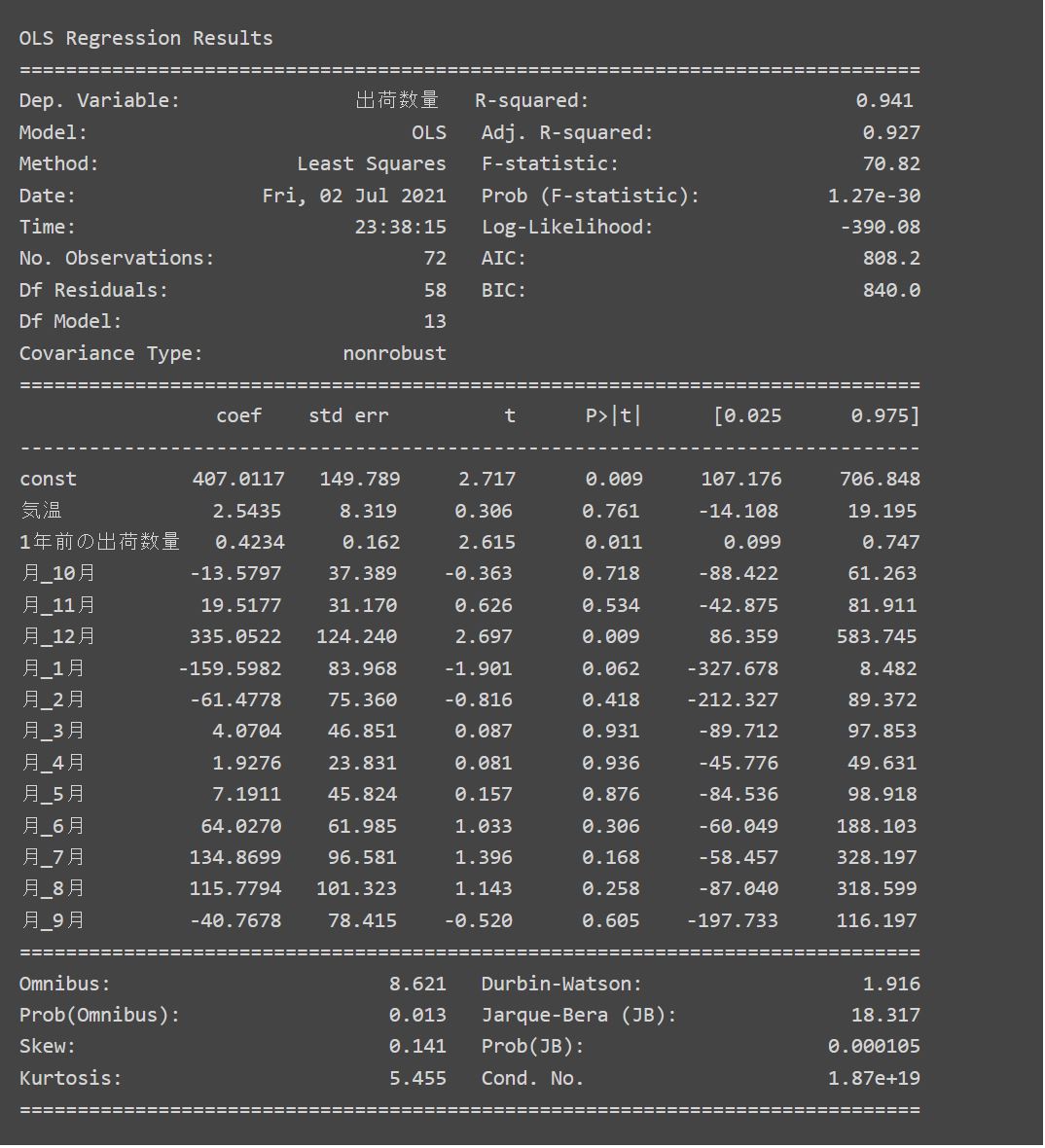
自由度調整済み決定係数(Adj. R-squared)が0.927となりました。1年前データの説明変数がない場合の同係数の0.924と比較し、わずかに改善しています。
さあ、新たな重回帰分析により予想精度はどの程度改善したのでしょうか?
④ 1年前データを説明変数に加えた場合の予想精度はどうか?
1年前の出荷量データを説明変数に加え回帰分析を行った場合の予想出荷数量と(グラフでは前相関ありと表記)、1年前の出荷量データを説明変数に加えずに回帰分析を行った場合の予想出荷数量と(グラフでは前相関なしと表記)を比較していきます。
次のグラフは、2つの重回帰分析より求めたスーパードライの予想出荷量と、実際の出荷量を折れ線グラフで表わしたものです。

グラフを見た印象としては、前相関なしの結果(橙色)と比較して、前相関ありの結果(水色)は、わずかに実際の結果(青色)に近いように見えます。
今回の回帰分析において、学習用データから除外した2018年8月から2019年7月の期間のみを拡大したグラフでも見てみます。

2019年2月のみ、前相関ありの結果(水色)のほうが、わずかに誤差が大きい結果となっていますが、それ以外の月では前相関ありの結果(水色)のほうが誤差が小さい結果となっていることが分かります。
それでは、定量的にはどうでしょうか?
ここでは、
誤差量 =(推定される出荷数量ー実際の出荷数量)÷ 実際の出荷数量
として誤差を求め、比較していきます。
| 誤差量 | 前相関なし | 前相関あり |
|---|---|---|
| 平均 | 16.6% | 10.4% |
| 標準偏差 | 8.29% | 8.05% |
| 最小 | 3.7% | 0.5% |
| 1/4分位数 | 12.2% | 2.6% |
| 3/4分位数 | 19.8% | 14.7% |
| 最大 | 33.5% | 24.5% |
前相関を用いずに予想したスーパードライの出荷量の誤差は、平均16.6%、最大33.5%となりました。一方、前相関を用いて予想したスーパードライの出荷量の誤差は、平均10.4%、最大24.5%となりました。
このことより、1年前の出荷量データを説明変数に加え回帰分析を行った場合のほうが、予測精度は改善する結果となりました。
まとめ
今回の記事では「重回帰分析で将来のビールの出荷量を予測してみる」というテーマで、重回帰分析を用いて将来のデータを予測する方法について紹介していきました。
年ダミーのような、過去のデータにしか現れない説明変数は、将来を予想する回帰分析では使えないことを説明しました。そして、代替え手段として、時系列分析で使われるコレログラムを用いました。
コレログラムにより、12か月前のデータと自己相関が高いことが分かったため、12か月前の出荷量データを新たな説明変数として加え、重回帰分析を行いました。
1年前の出荷量データを説明変数に加え重回帰分析を行うことで、1年前の出荷量データを用いずに分析した場合と比較し1年間の平均で6.2% 出荷量の予想誤差を低減し、その予想誤差は平均10.4%という結果となりました。
このように時系列分析においては、過去のデータとの自己相関性を見出すことで、将来の予測の精度を上げられる可能性があります。そして、今回の例では、月単位での自己相関性を見ましたが、月単位だけでなく、週・日・時間単位でも自己相関性を見ることはできます。
さて、最後に、今回の分析のサマリでは「Cond. No. : 1.87e+19」となっており、前回記事の分析結果と同様に多重共線性が強い状態となっております。
このままでは予測の精度が低くなってしまう可能性があります。ということで、多重共線性についての説明と、その影響を低減させた場合の予測結果については、次回の記事で紹介したいと思います。
じゃあ
















