別記事「気温が上がるとビールの出荷量は増えるのか?」では、気温が1℃高くなると、何本ビールの出荷量が増えるか?をという推測を、過去のデータを用いた単回帰分析で求めました。
そして、平均気温とビールの出荷量の関係には、12月を考慮から取り除いた場合に限り、気温が1℃高くなると、月当たりのビールの出荷量が大瓶382万本増える結果を得ることが出来たことを紹介しました。
一方で、12月を含めたビールの出荷量は、気温だけでは推測が難しくなるため、説明変数を増やす必要があることも書きました。
ということで、今回の記事では、
- 複数の説明変数を用いた重回帰分析の流れについて興味がある
- 重回帰分析で得られた推定値と実際の値に、どの程度の違いが生じるかを見てみたい
という人に向けて、「重回帰分析で求められるビールの出荷量の精度は?」というテーマで、重回帰分析を行っていく流れと、得られた回帰式の精度について紹介していきます。
重回帰分析で求められるビールの出荷量の予測精度は?

重回帰分析でビール出荷量を予想してみる
① 目的変数はスーパードライの出荷数量
今回の分析も、アサヒスーパードライの2011年8月から2019年7月までの8年間(96か月分)の出荷量のデータを用います。ここでのひと箱は大瓶(633ml)×20本を指します。
次のグラフは、年月を横軸とし、スーパードライの出荷量を折れ線グラフで表わしたものです。
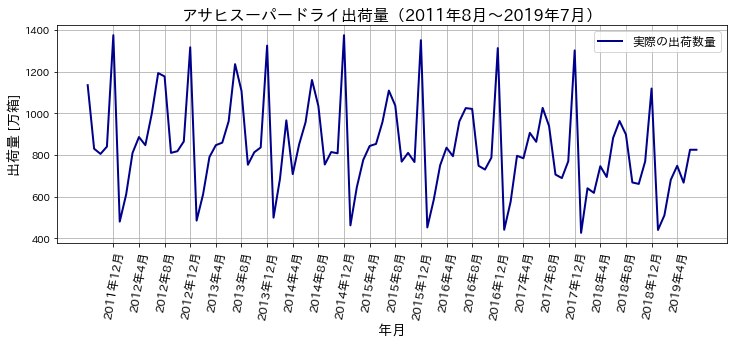
今回の分析では、目的変数をスーパードライの出荷量 と設定して、重回帰分析を行っていきます。
② 説明変数のダミー変数化について
今回は、別記事「気温が上がるとビールの出荷量は増えるのか?」の続きということで、出荷量データと東京都の平均気温の2つのデータのみを用いて重回帰分析を行うことを考えます。
従って、説明変数は、下記3データを用いることとします。
- 平均気温(東京都)
- 月データ
- 年データ
上に挙げた説明変数を用いた重回帰分析を行う際に、注意すべき点があります。
それは、月データと年データは「間隔尺度」であるということです。
なぜ注意が必要になるかと言うと、たとえば、12月は6月の2倍の関係にあるわけではないことから、12月というデータを12という数字データとして扱うことは出来ません。
そのため、数値データとして扱うことの出来ない説明変数は、「ダミー変数」としたうえで分析を行う必要があります。
ダミー変数化を行うと、「12月ダミー」のような説明変数が新たに作られ、12月の場合は「1」、12月でない場合は「0」の数値データが割り当てられることになります。
今回、「平均気温」「年」「月」の3つの説明変数で重回帰分析を行うこと考えましたが、ダミー変数化により、「年」の説明変数は2011年から2019年までの9つのダミー変数に置き換えられ、「月」の説明変数は1月から12月までの12つのダミー変数に置き換えられることになります。
従って、計22つの説明変数で重回帰分析を行うこととなります。
③ 単回帰分析と比較して重回帰分析の結果はどうか?
ダミー変数化を行ったうえで、「平均気温(1つ)」「各年(9つ)」「各月(12つ)」の22つの説明変数で、重回帰分析を行います。
分析は最小二乗法(OLS)で行います。次のログは分析結果のサマリです。
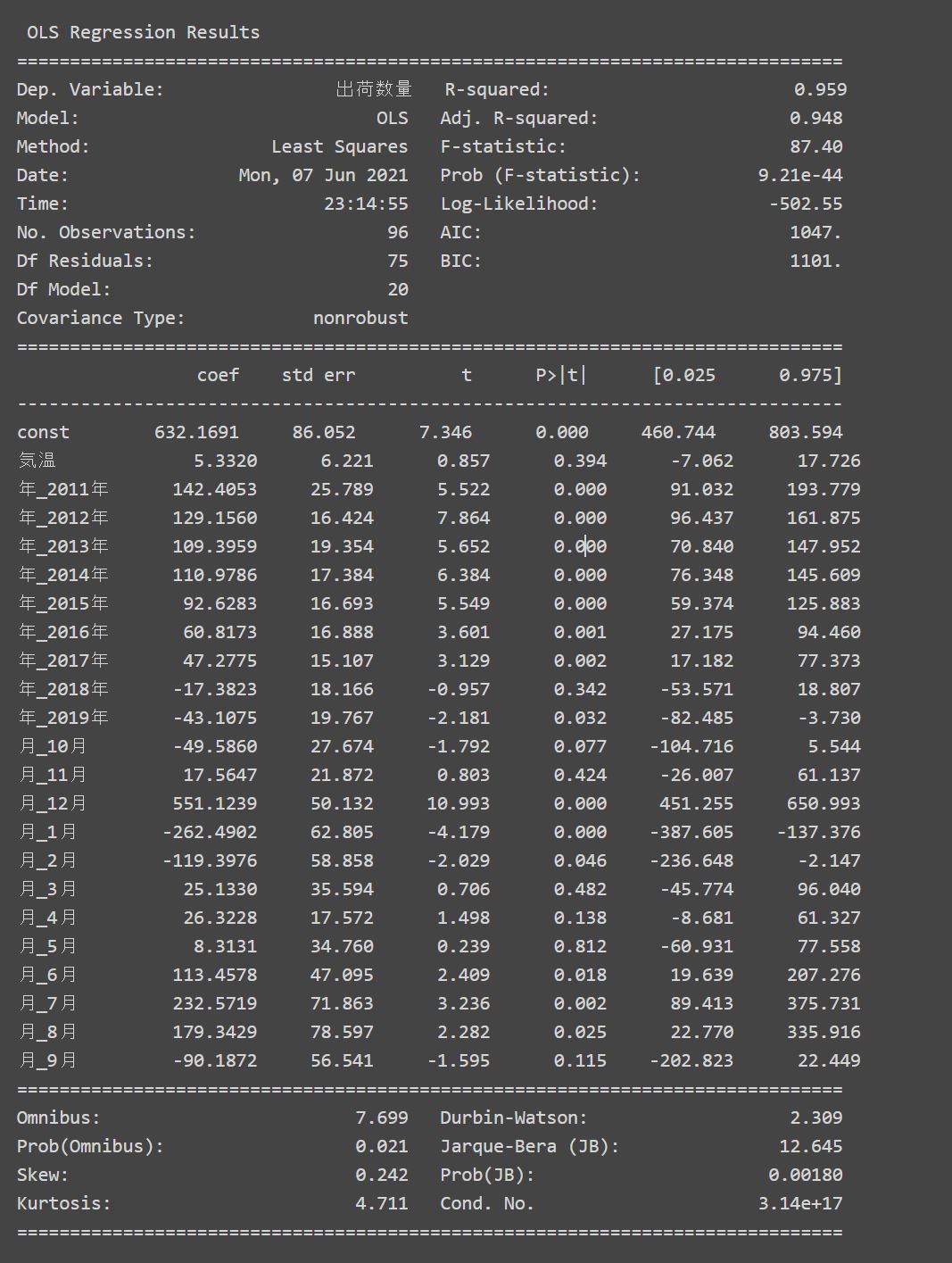
自由度調整済み決定係数(Adj. R-squared)に着目すると0.948とあります。
別記事「気温が上がるとビールの出荷量は増えるのか?」で行った単回帰分析における決定係数0.623であったことより、今回の重回帰分析が前回の単回帰分析より高い精度の回帰式を得ることができました。
なお、回帰分析のサマリの読み方に関しては、別記事「あなたはどのぐらい分かる?回帰分析のサマリの読み方」で紹介しております。
④ 重回帰分析により得られた回帰式の精度はどうか?
重回帰分析により、回帰式を得ることができました。
それでは、回帰式より求められる推定値と実際の値はどの程度の違いがあるのでしょうか?
次のグラフは、得られた回帰式を用いて、ビールの出荷量を推定したものを折れ線グラフで表わしたものです。

グラフを見た印象としては、予実の差がある月もありますが、全体的にはフィットしているようにも見えます。
定量的にはどうでしょうか?
ここでは、
誤差量 =(推定される出荷数量ー実際の出荷数量)÷ 実際の出荷数量
として誤差の程度を求めていきます。
| 誤差量 | 数値 | 備考 |
|---|---|---|
| 平均 | +0.2% | 96か月分 |
| 標準偏差 | 6.0% | – |
| 最小 | -19.0% | 2019年1月 |
| 1/4分位数 | -2.2% | – |
| 3/4分位数 | +3.5% | – |
| 最大 | +20.0% | 2014年4月 |
この結果より、95%信頼区間で考えると、おおよそ±12%の誤差範囲で、ビールの出荷数量を推定できることが分かりました。
誤差の範囲が±12%ということで、もし、この回帰式を用いてビールの生産計画を立てることを考えた場合、ビールの生産には原材料の確保なども必要となることなどの理由から、±12%の誤差は決して精度の高い数字だとは言えませんが、ざっくりとした傾向を求めるような用途であれば、許容できる誤差と言えるかもしれません。
⑤ 今回の回帰式は、実は使い物にならない
重回帰分析を行い、ある程度の精度(誤差)で出荷数量を推定できることが分かりました。
しかし、残念ながら今回重回帰分析で求めた回帰式では将来の出荷数量を推定することは出来ません。
理由は、説明変数として「各年のダミー変数」を用いているためです。
今回得られた回帰式には、例えば、2020年のダミー変数はありません。そのため、2020年以降の出荷数量を推測することは出来ません(正確には、出荷量は推定できますが、精度は下がります)
また、今回の重回帰分析の結果は「多重共線性」が強いことも問題となります。
多重共線性が強いとは、説明変数間の相関係数が高い場合に発生する現象であり、この状況下では、回帰係数の値が入力データの変化に不安定になってしまうことから、適切な回帰式が得られない可能性が高いことを示唆します。
分析のサマリの中で「Cond. No. : 3.14e+17」と記載の箇所が、多重共線性が強いことを示しておりますが、その点については、また別の記事で触れていきたいと思います。
まとめ
今回の記事では「重回帰分析で求められるビールの出荷量の精度は?」というテーマで、重回帰分析を行う流れとその結果について紹介しました。
重回帰分析を用いることで、平均気温データのみを用いた単回帰分析より精度の高い回帰式を得ることが出来ました。
また、重回帰分析を行う際に、数値データでない説明変数に対してはダミー変数化を行う必要があることを紹介しました。
重回帰分析を用いることで、信頼区間95%において±12%の誤差範囲の回帰式を得ることが出来た一方で、今回の回帰式には強い多重共線性が発生していることと、将来の出荷量を求めることは出来ないため、まだ課題があります。
長くなったので、将来の出荷量を推測するための手法については、また別の記事で紹介したいと思います。
じゃあ。

















